Projects
Industrial Sponsorship
Dynamic Performance Investigation of Base Isolated Structures
By Ather K. Sharif
8.1 Introduction
This chapter examines the dynamic performance of a Base Isolated Structure known as Apex Plaza in Reading. This office building was constructed around 1986 adjacent to Reading main line railway station. The development consisted of four blocks served by a central atrium shown in Figure 8.1.
Owing to the large size of the site, only the blocks nearest to the railway required base isolation, with the furthest blocks having traditional foundations. This provided a unique opportunity to compare identical buildings, with and without base isolation.
The dynamic characteristics of these structures were established using train pass-by and ambient conditions, as well as under excitation provided by impact testing and a shaker. Finite element models were also produced to correlate with some of the characteristics that were measured.
8.2 The Railway
Reading Railway Station is a major interchange. The tracks were jointed in parts with numerous points. The tracks carry a range of trains including local passenger, inter-cities and freight.
Figure 8.1 shows the proximity of the office blocks to the railway tracks. The closest distance of the building to the nearest railway sidings is about 15m. The distance from the main tracks was 20m or more. The numerous railway tracks totalling 16 in number were built on a man made embankment. Just east of the site there is a railway bridge, crossing Vastern Road.
8.3 Ground Conditions and Foundations
This consists of made ground overlying some variable clay onto gravel overlying soft 'weathered' chalk becoming hard with depth. The development entailed removing the majority of the made ground. Augered cast in situ piles of 1m diameter were sunk to a bearing depth of 18m onto the hard chalk. The pile caps were formed in the variable clay and top section of gravel. Figure 8.47 shows a soil section which indicates the relative position of a typical pile. The water table was high, at just below pile cap level.
8.4 The Building
The four blocks served by a central atrium, consisted of a basement used for car parking and ground floor to sixth floor used as offices. Each block was approximately 68m in length, 15m in width and 30m in height, shown in Figures 8.1 and 8.2.
The building was constructed with an in situ concrete frame and trough slab floors. The total mass of each block was in the region of 8000 tonnes (dead load), including the two staircase cores at each end. The building was clad with aluminium and glass, which was fixed to the face of edge beams and columns.
Internally the building was finished with a heavy raised floor (steel encapsulated concrete panels) and false ceilings. The building was air conditioned, with cooling towers on the roof, as well as satellite modular plant rooms in the central core areas on every floor, serving each block and floor independently.
Plate 8.1 shows a general view of a model of the building. Plate 8.2 shows a view from the roundabout on Forbury Road. Plate 8.3 shows an internal view of the atrium, with the un-isolated connecting core in the foreground, between the isolated and un-isolated blocks. Plate 8.4 indicates the type of rubber bearings and layout used at pile cap level.
8.5 Measurement Parameters
In initial 'free-field' site surveys, the measurement parameter was peak particle velocity, PPV, quoted as zero to peak in mm/sec. This was originally recorded using geophones, which was favoured by the consultants (Crockett and Associate, 1984). The Author was concerned about inaccuracies due to low frequency digital correction used to extend the frequency range through the geophones' resonance. In the measurements on the completed building, all measurements are therefore undertaken using accelerometers. Results are in terms of acceleration in mm/s2 units.
8.6 Vibration and Noise Environment
During 1984, the Author undertook vibration measurements on the vacant site, originally used as a car park. Measurements were taken in a pathway, which was at the boundary of the site. Levels varied from 0.2mm/sec to 0.75 mm/sec in the vertical direction and 0.2mm/sec to 0.9mm/sec in the radial direction. These levels bordered just perceptible to easily noticeable. At 10m from the boundary of the site, vibration levels dropped to 0.1mm/sec to 0.35mm/sec, where they were only just perceptible. The highest levels being due to the non-stop inter-city trains which had a pass-by duration of 8 seconds and dominant frequencies mainly around 18Hz. Freight trains were of much longer pass-by duration, and caused lower dominant frequencies.
It was recognised that these 'free-field' ground vibration levels would be reduced by the inertia of the proposed building. To obtain some information on this transfer function, into a heavy piled building which is un-isolated, measurements were taken at a nearby building, known as Metal Box, which is to the east of the site and shown in the keyplan of Figure 8.1.
The peak vibration levels taken from time histories on the un-isolated column of this neighbouring building were found to be reduced by a value of around 70% from the nearby 'free-field' ground measurements (see Sharif, 1999).
Airborne noise was also measured in detail and used to specify the sound reduction index for the cladding. Interestingly, the public address system used for station announcements created a very significant level of noise. Diesel locomotives also frequently engulfed the site in fumes.
Despite these environmental impacts, this was a prime site, adjacent to the mainline station in the heart of Reading. It therefore provided an opportunity for high rents, provided the building could achieve a good quality internal environment.
8.7 Empirical Prediction of Building Response
The 'free-field' ground vibration levels are often reduced to account for the effect of the inertia of the building. The empirical reduction used can usually vary from 30 - 60%. In the case of the nearby Metal Box building, the reduction of peak levels was generally as high as 70%. The adjusted vibration levels can then be magnified by a factor of 2 to 3 times to allow for resonances in floors.
Such predicted levels were assessed in terms of human perceptibility and the potential for groundborne noise.
The aspect of human perception is nowadays dealt with using response curves given in a British Standard (BS 6472, 1992) where acceleration is the preferred measurement. However at the time of this development, assessment was based upon velocity measurements compared with the simple scale proposed by Reiher and Meister (1931).
Groundborne noise predictions were based on simple models which rely on calculating sound pressure from a radiating surface (see Grootenhuis, 1982). The resulting noise levels were assessed in terms of not only their absolute values, but also how much higher they were compared to the background.
Such empirical predictions (Crockett and Associate, 1985) indicated that vibration within a traditionally founded structure would be perceptible for inter-city trains which passed through the station at speed. A railway bridge carrying all the tracks over a road also adjoins the site and is founded into the chalk, onto which stratum piles for the new building were to be founded. This presented a good path for 'audio' frequency transmission into the structure. There was therefore a risk that in private offices and conference rooms, groundborne noise may have been detected.
In order to attenuate these effects base isolation was adopted, although modified predictions of the resulting environment with this proposed foundation system were limited at the time.
8.8 Isolation of the Closest Office Blocks
As vibration decayed with distance away from the railway, it was deemed appropriate to provide base isolation for the two blocks nearest the railway. The two blocks further away, and the connecting core areas, providing staircase and lifts were un-isolated.
Whilst vibration decays with distance due to geometric and material damping in the ground, it is known (ISO 4866 Annex F, 1990) that buildings in the path cause additional attenuation, as they absorb energy from the ground, dissipating it as heat in the structure and its contents.
One would in principle expect less screening from a base isolated building, as the screening mechanism entails the building absorbing energy from the ground, a situation which should be inhibited by the isolators.
However, as the comparative screening effects of isolated and un-isolated buildings in the path was not quantifiable, this mechanism was ignored when predicting levels 'downstream' of the isolated blocks.
Block 'C' (shown in the keyplan of Figure 8.1) was base isolated using laminated natural rubber bearings to produce a ‘rigid body’ vertical natural frequency of about 7.5Hz. These bearings were located on the pile cap.
Figure 8.3(a) shows a typical layout of rubber bearings for the isolated columns on gridline "A" for Block 'C'. Figure 8.3(b) shows how additional bearings were arranged for the heavier columns on gridline "B".
The rubber bearings were simply parked in position on the pile cap (see Plate 8.4). Figure 8.3(c) describes how a precast concrete 'hat' was then lowered onto the bearings. The precast 'hat' had slots for precast beams, which were lowered into position and interlocked with neighbouring precast 'hats' on adjoining pilecaps. Concrete was then poured into the trough of the precast 'hat', which interlocked the precast beams and provided starter bars for the in-situ concrete column.
The precast 'hats' were provided with downstand concrete snubbers (shown in section in Figure 8.3(a)) that would seat on the pile cap in the event of failure of the rubber bearings. This downstand encircled the rubber bearings preventing any direct views on the bearings. To enable inspection of the bearings, holes were provided in the downstand, through which a fibre-optic endoscope could be used to view all the faces of the bearings. It was recognised that such a downstand detail would inhibit easy replacement of bearings, although it was envisaged that failure was very unlikely. If it were to occur, part of the downstand could be cut away, after having provided some temporary propping with a jacking arrangement, to allow insertion of new bearings.
Taking a typical cross section on gridline 15, we can see the variation of unfactored dead load at pile cap level, the number of bearings provided, along with the expected dead load deflection in Table 8.1.
Table 8.1 Dead Load and Isolator Details
|
|
|||
|
|
|
|
|
| Unfactored Dead Load (tonnes) |
|
|
|
| No. of Bearings |
|
|
|
| Size (mm) |
|
|
|
| Expected Mean Deflection (mm) |
|
|
|
Block 'A' was similarly mounted, but with a design 'rigid body' vertical natural frequency of 9.5Hz. The higher natural frequency was adopted to economise on the cost of the isolators, given that Block 'A' was subject to lower vibration levels, being further from the points in the tracks.
An economy on the supply cost of the isolators arose, because the higher natural frequency required thinner bearings, with an unloaded height of 168mm. This provided a deflection under load of 8.3mm. (This saving on the supply cost of the isolators would probably have been reduced by additional costs during construction to cope with the varied specification, but was driven by the developer, to minimise initial costs.)
Each block had a staircase core at each end, which was also isolated on rubber bearings at pile cap level. At this location wind sway control devices were provided to restrain horizontal and rocking motion. Typical details are shown for staircase number '3' for Block 'C' in Figure 8.4(a).
The isolated block adjoins a central un-isolated core, providing lifts and staircases, as well as modular plant rooms. This un-isolated core is used to provide lateral restraint on upper floors, levels 2, 5, 6 and 7 using rubber bearings shown in Figure 8.4(b).
The atrium roof was formed as a steel truss and spans across the un-isolated and isolated blocks. It was resiliently mounted on rubber bearings to provide unrestricted thermal movements, to accommodate horizontal differential motion of the blocks under wind sway, as well as avoid any rigid contact with the isolated blocks.
The overall additional cost of base isolation was estimated at 3-4% of the main contractor's tender value (relating to the isolated blocks) which represent not just the cost of the isolators but the knock on effects on construction.
8.8.1 Rubber Bearings
Laminated natural rubber bearings to support the building were provided by BTR. They quoted a critical damping ratio of 3-5%. Dynamic stiffness was to be taken as 1.8 times static (tangent) stiffness at the working load. Synthetic rubber bearings supplied by TICO, were used in the wind sway control devices and the atrium roof supports.
8.9 Dynamic Performance Survey Procedure
The buildings have now been occupied for some 10 years and there have been no adverse comments. When the building was complete, the Author undertook detailed vibration measurements on separate occasions. These measurements were taken late at night to avoid recording vibration due to occupants.
Detailed site inspections were also undertaken in the sub-basement void, using a fibre-optic endoscope and steel rods to check continuity of air gaps. Surprisingly, short circuits were discovered in a few columns, which were caused by a small amount of cement grout bridging gaps (see section 8.11).
Groundborne noise in the isolated buildings was not observed above background levels of air conditioning noise, and would have been masked by the airborne paths anyway. The performance of these isolated buildings in terms of groundborne noise could therefore not be investigated.
8.9.1 Instrumentation
Final measurements following detailed site inspections were undertaken in 1997, using a PC based monitoring system described fully in Chapter 6. This consisted of four BandK 4378 accelerometers connected to BandK 2635 charge amplifiers fed to a National Instruments data acquisition card. All accelerometers in the system were calibrated in situ using a portable BandK calibrator type 4294. Data acquisition was controlled and viewed using a program written by the Author in LabVIEW. Post-processing was undertaken using MATLAB®.
8.9.2 Measurement Locations
Figure 8.1 provides the gridline references used for measurement locations, and Figure 8.2 shows a section indicating the positions at which vibration measurements were taken in various set ups. These consisted of vertical (V), Longitudinal (L) and tangential (T) measurements at a number of positions. Longitudinal was defined as being perpendicular to the tracks and tangential being parallel. Measurements were undertaken on ground slabs, pile caps, base and top of isolated / un-isolated structures, including the midspan of floors (Sharif, 1999 for more detailed collection of results).
8.10 Correlation of Inputs
Hunt (1996) has emphasised the need to consider the correlation of inputs when modelling vibration transmission into buildings, and Cryer (1994) has shown this to be highly relevant in the case of modelling base isolated buildings.
Ideally the correlation of inputs to a building should be examined with measurement on pile caps in absence of the superstructure, as this can influence the results. However this was not possible in this case study and we therefore can only examine the coherence of vibration measurements on different pile caps with the structure in place. Figure 8.5 shows time history of vertical vibration measurements on pile caps on gridlines 15, A, B, and C at increasing distance from the railway tracks, as well as measurements on gridline A13 representing a different section (see Figure 8.1 and 8.2).
Figure 8.6(a) shows the coherence of vertical measurements between pile caps at A15:B15 and A15:C15. There is higher coherence at low frequencies, and this tends to diminish as the comparisons are made between more distant pile caps. Figure 8.6(b) shows the same comparison but for horizontal measurements at right angles to the railway. The larger coherence at low frequencies is more evident, and a reduction in coherence again occurs when comparisons are made between more distant pile caps. Figure 8.6(c) shows repeat performance for a direction parallel to the railway tracks.
Coherence, which can be used to examine the correlation of inputs to a building, is seen to be larger at low frequencies, and this tends to diminish with increasing separation of distance between pile caps. The coherence in the horizontal axis, in particular at right angles from the track tends to be higher in this case. Coherence would be relevant in the theoretical modelling of inputs to a structure (see Cryer, 1994).
8.11 Effect of Short Circuits in Base Isolation System
It was known that during construction the contractor would use Korkpak, polystyrene, or plywood sheets as temporary shuttering, and these can sometimes be left in place. Often this occurs by poor design of construction method, where subsequent lack of access inhibits removal. The snubber air gap between the pile cap and the failsafe downstand snubbers can also become filled with debris.
The Author therefore undertook a thorough inspection in the sub-basement void. A fibre-optic endoscope was used to inspect the bearings and gaps on every column. Steel rods were used to check that air gaps were continuous, wherever they were required. This inspection revealed a very alarming result. On some areas, a small amount of concrete grout had penetrated a section of the snubber air gap, thereby allowing a short circuit. Figure 8.7(a) shows the most serious of the short circuits found, which was under column C13, where a small amount of cement grout bridged the gap. Figure 8.7(b) shows an example of a minor short circuit.
The design of the precast 'hat' assembly system would not have allowed in-situ concrete to penetrate the bearings or the air gaps. However the precast beams were inadequately reinforced, which was attributed to a design mistake by the precast concrete suppliers. This caused shear cracking to be witnessed in these beams during construction. The contractor's solution was to increase the size of precast beams at the precast 'hats' by casting an enlarged section. This enlarged section encompassed some of the inspection holes, which were inadequately caulked to prevent grout ingress under pressure. The result is that this short circuit remained invisible externally, and could only be detected using the fibre-optic endoscope and rodding.
The grout was found to be largely laminated and loose, although it would cast doubt on some of the measurements. A finite element model of this grout showed that it could, owing to its thin height, significantly contribute to an increased stiffness.
The effect of the grout short circuit between the pile cap and base of isolated column was investigated by comparing measurements on identical isolated columns at the same distance from the railway tracks, except where one was free of any short circuits and one with the a short circuit. Performance of isolated columns is judged relative to the respective pile caps, although this does not provide actual insertion loss for base isolation.
Figure 8.8 shows the direct transmissibility from respective pile caps to the base of the isolated columns. The solid line refers to the direct transmissibility across the free isolated column (C15), and the dashed line for the short circuited column (C13). There is a good deal of similarity, except for some small evidence of improved performance for the free column. Figure 8.9 shows similar comparisons from the pile cap to the base of the columns but in one horizontal direction. Again there is a good deal of similarity with some evidence of improved performance for the free column. Direct transmissibility from pile cap to the top of these columns are also compared in Figure 8.10 which shows similarity.
An example of a more minor short circuit was also investigated as seen in Figure 8.7(b) for column B5 in isolated Block A which had a slightly higher target base isolation frequency of 9.5Hz. The performance of a neighbouring isolated column (B4), free of any short circuits was used for comparison. Figure 8.11, across the base, shows that there is slightly better performance for the free column, although difference in transmissibility to the top of the columns shown in Figure 8.12 is less.
Since the concrete grout has caused short circuits to the base isolation system, a comparison in performance of neighbouring isolated columns, free and short-circuited using direct transmissibilities should indicate the effect of the short circuit directly. Yet the results between free and short circuited columns were broadly similar. The free column indicated some evidence of improved performance over the short circuited columns, particularly in comparisons to the base of the columns and less so in comparisons to the top of the columns.
The Author could not remove these short circuits using rodding. The integrity of the concrete grout that formed the short circuit is likely to be affected by the differential temperature cycling of the isolated building compared to the cooler more constant temperatures in the sub-basement, as well as effects of differential drying out shrinkage movements in the concrete. This could well work the joint, and may in some cases lead to a fracture in the short circuit. Only a minute air gap would be needed to render a short circuit ineffective, when considering the small dynamic displacements that arise under rail excitation. This may have occurred here, as early measurements by the Author, soon after construction, (see Sharif, 1999) indicated that the short circuits were very influential in causing the response of the base of the column to move in unison with the pile cap below. Such a situation in these latter measurements was not repeated.
All the results in subsequent sections of this Chapter refer to columns that were not subjected to short circuits directly, although may of course be influenced by vibration coming through the short circuited path. Even so, the effects of these short circuits were not very dramatic, in comparison to the free isolated columns. These short circuits would ordinarily have gone unnoticed, only being unearthed by detailed inspections. Therefore the creation of short circuits remains a practical risk in the construction of base isolated structures.
8.12 Train pass-by and Background Measurements
The performance of isolated structures is judged relative to an input on the respective pile cap below, as these are often the only measurements possible, but does not provide the actual insertion loss for base isolation. This can only be inferred by comparing measurements on isolated and un-isolated structures that are otherwise similar. This section describes measurements of train pass-by and background samples on both isolated and un-isolated structures.
8.12.1 Isolated Column A15 (Block 'C')
Isolated column A15 is typical of the outer columns, which support the floors and external cladding. Simultaneous measurements were made on the pile cap, base of the isolated column and top of the isolated column.
Figure 8.13 shows part of a time history for a train pass-by with a sample of background vibration, on the right of this figure, taken late in the evening. The train vibration is clearly visible against the background levels on the pile cap, though less so on the base of the isolated column. The isolated column shakes more than the pile cap and base of the isolated column shakes more than the top of the isolated column in the background.
An estimate of the auto spectra is shown in Figure 8.14. This compares spectra for a train and background sample. On the pile cap, train signals significantly exceed the background levels. This figure also shows the noise floor of the instrumentation chain, which was discussed in Chapter 6.
The background levels have dominant peaks at 25Hz, 50Hz, and 100Hz. Whilst the peak at 50Hz and 100Hz is often associated with mains interference, relevant precautions (described in Chapter 6) were taken, and in this case it is attributable to services noise in the building. Most of the increase occurs at low frequencies, although around and above 80Hz, the train signals do not exceed the background levels in the isolated column. Such a situation is characteristic of a railway source at grade, which tend to propagate energy at low frequencies, which makes it impossible to evaluate performance at high frequencies because of masking by background noise.
Figure 8.15 shows the total and direct transmissibilities from the pile cap to the base of the isolated column for a train event. The first mode resonance reaches 16dB at 8Hz, with some isolation visible between 20Hz and 100Hz reaching 19dB at 60Hz, but there are many reduced attenuation peaks.
Figure 8.16 shows the total and direct transmissibilities from the pile cap to the top of this isolated column for the same train event. Here the first mode resonance reaches 21dB and again occurs at 8Hz, with some isolation evident above 20Hz and up to 100Hz, reaching 20dB at 65Hz, although there are many resonance peaks. Above 100Hz, the curve ramps due to poor train signal strength in relation to background.
Differences between total and direct transmissibilities implies that response of a column is not solely due to input from the pile cap below, but affected either by vibration from services noise, or uncorrelated vibration from other paths (e.g. neighbouring pile caps/columns).
Figure 8.17 compares total transmissibilities from the pile cap to the top and base of this isolated column. The results are very similar at the low frequency end of the spectrum. We see that a reduction of pile cap levels can arise above 20Hz and therefore the situation at lower frequencies, which is characteristic of railway sources at grade (particularly freight) would in fact be made worse due to resonances below this range.
We can compare the total transmissibilities for both a train event and background sample in Figure 8.18 from pile cap to top of isolated column. This shows that at the first mode resonance, the transmissibilities for a train and background event are similar. In the case of the background sample, the low frequency resonance peak is limited by damping. For a train pass-by the peaks are again limited by damping to the same extent, and therefore explain why the low frequency peak under ambient and train pass-by do not alter much in shape and size. However, significant differences arise above this first mode resonance. We can see that the train event transmissibility approaches the background situation at higher frequencies. The shape and magnitude of transmissibility curves are therefore dependent upon not only the system characteristics, but also how strong the train vibration signal is compared to the background. It is therefore clear that the strength of the train signal, in relation to background levels, can affect the amount of isolation that is visible.
The repeatability of the total transmissibility curves for five different train events, from pile cap to base of isolated column, is shown in Figure 8.19. Better repeatability between individual train events was found to occur to the base of the isolated column, than to the top, from the pile cap below, as seen by comparing Figure 8.19 with Figure 8.20. This is because transmissibilities to the top are more influenced by variation in background levels, and vibration from other paths that may be more train dependent.
The total transmissibilities for different background samples were found to show a large variation for records taken at different times of the night. The top of this isolated column responded up to 40 dB more than the pile cap, under ambient conditions (see Sharif, 1999). Services plant was found to be coming on and off at various times, affecting the ambient vibration of the isolated structure. Measurements wherever possible were taken when background levels were at their lowest. This required measurements to be taken very late in the night, and even that did not guarantee that all the plant would be off. During daytime with occupants' footfalls, lifts, building maintenance and plant under greater demand would clearly have made results unusable.
8.12.2 Comparison of Isolated Columns A15 and B15 with Isolated Staircase '3'
It is interesting to compare the behaviour of isolated column A15 with a neighbouring isolated column B15. Column A15 has been described as typical of an outer column supporting floors and the cladding, with a total mass at foundation level of 228 tonnes. Column B15 is typical of an inner column, supporting floors only, although for a larger floor area, and therefore a greater supported mass of 482 tonnes. The same target rigid body vertical natural frequency of 7.5Hz was achieved using two rubber bearings in the case of column A15, shown in Figure 8.3(a), whereas column B15 required four rubber bearings, shown in Figure 8.3(b). Column B15 is a further 6.2m from the railway tracks, shown in Figure 8.2. This difference in distance is less relevant, as we are not comparing absolute values, but relative values compared to the supporting pile cap.
It was also interesting to examine the behaviour of a staircase, as it represented a stiff concrete spine, which was used to provide wind sway restraints.
Comparisons of the mean total transmissibilities of isolated columns A15 and B15, with the isolated staircase are made. This is shown in Figure 8.21 (pile cap to base) where the low frequency resonance modes are similar, peaking at 10 to 15dB, with isolation becoming evident above 20Hz. The staircase largely shows deeper attenuation than the columns. Figure 8.22 shows the total transmissibilities (from pile cap to top), where there is again some similarity at low frequencies, with generally larger attenuation for the staircase between 20Hz and 100Hz. Reduced attenuation peaks arise in all cases, but are generally less pronounced in the staircase. The apparently more rigid construction of the staircase, with continuous concrete walls, which represents a stiff spine compared to the framed building, does not itself perform significantly better than the isolated column. This implies that whilst it is desirable in principle to approach a rigid body design and thereby avoid resonant modes, this situation could not be avoided in practice even from a box type structure of a staircase core area. The similarity of the staircase results to the isolated column also show that the deployment of wind sway control devices (see figure 8.4(a)), did not adversely effect staircase performance.
Comparative behaviour above 100Hz can be ignored, as it is adversely affected by background vibration, where train vibration levels are so low as to be of no significance.
8.12.3 Comparison of Isolated Column B3 (target 9.5Hz) with Isolated Column B15 (target 7.5Hz)
Two identical office blocks were isolated, with Block 'A' base isolated using a higher target rigid body vertical natural frequency of 9.5Hz, compared to Block 'C' at 7.5Hz. The higher target natural frequency was achieved using thinner, stiffer bearings in the case of Block 'A', which required a lower degree of isolation, owing to its greater distance from points in the track. It is interesting to see if a difference in performance is borne out by the results.
This section compares measurements on isolated column B3, for Block 'A', which is identical in every other respect to isolated column B15 in Block 'C'.
A comparison of transmissibilities to the top is shown in Figure 8.23. The two isolated columns show the characteristic low frequency peak, where isolated column B15 has the first mode peak about 0.6Hz lower than isolated column B3. This difference in the position of the peaks is not as great as the difference in the target natural frequencies aimed for. As a result of requirements to achieve a given statistical confidence in the auto spectra estimates, there is a limitation in resolving frequencies, described in Chapter 6. The effective bandwidth of the spectral window achieved is 1.79Hz, which limits our ability to resolve small changes in frequency accurately.
The low frequency modes peak at 20dB in both cases. Column B15 shows a distinct peak at 11Hz, which is only just visible in column B3. Between 20Hz and 100Hz, both columns exhibit some isolation, although B15 does indicate a higher degree of isolation.
This set of comparisons implies that a higher degree of isolation is possible from a lower rigid body natural frequency.
8.12.4 Comparison of the response of the top and base of isolated columns
Figure 8.24 compares the low frequency response of the top and the base of isolated columns A15, B15, B3 and staircase 3 for a train pass-by, which invariably indicates that the top of these structures responds more than their base, when referred to their respective pile caps. This can be due to a fixed-free mode of the structure.
8.12.5 Comparison of Isolated Column C15 and adjoining Un-isolated Core
This site provided a unique opportunity to compare the response of similar isolated and un-isolated structures, which should indicate the insertion loss for base isolation. The response of the isolated column, grid reference C15, is compared with the adjoining un-isolated core area. The two structures were separated by an air gap with no rigid connections bridging the gap, other than the resilient floor level wind restraints, and resilient fire stops shown in Figure 8.4(b).
The two structures have dissimilar sections. The isolated column being a concrete column supporting office floors, whereas the core area is a continuous wall supporting plant rooms on each floor (see Figure 8.1). Nonetheless, they are both of identical height, constructed in concrete, and at the same distance from the railway. It is therefore interesting to examine the degree of difference in their response. Measurements are presented for the top and base of the un-isolated core and isolated column. Figure 8.25 shows time histories for a train pass-by. It is very interesting to see that the isolated and un-isolated structures both respond with similar magnitude, at the base (traces (b) and (c)) and top (traces (a) and (d)) reference points. Yet one is base isolated and the other is not. Leaving aside the differences in the member section sizes and floor loading of the isolated column and un-isolated core, a lower level of response would have been expected for the base isolated structure.
The total transmissibilities from the un-isolated core to the isolated column, across the top and base reference points, are compared in Figure 8.26. There are differences between the two, but the general picture is that the isolated column shakes more than the un-isolated core. Curiously, between 20Hz and 40Hz, at which the train spectra is high, at one set of frequencies the comparison across the top indicates amplification, yet isolation is seen across the base. This situation is reversed in the neighbouring set of frequencies. This is likely to be due to the different mode shapes that arise.
Figure 8.27 shows a similar set of comparisons in the horizontal plane, in the Longitudinal direction, where there is seen to be some benefit across the top of the structures between 20Hz and 40Hz.
8.12.6 Comparison of Un-isolated Core to Isolated Columns (Block 'A' and 'C')
We can compare the mean total transmissibilities for five train events, from the un-isolated core to the isolated column, for both Block 'A' and Block 'C'. The mean total transmissibilities across the base are shown in Figure 8.28(a), which describes broad similarities in the results for the two blocks. A similar conclusion can be drawn from inspection of the results across the top, shown in Figure 8.28(b). Across the top, the isolated column shakes more than the un-isolated core at 8Hz and 22Hz in the low frequency region. Generally there is little benefit to be seen from base isolation.
These results indicate that base isolation does not provide any material benefit, above that which would have arisen in traditional founded construction. This observation is however limited to the extent that whilst the isolated structure and adjoining un-isolated core adjoin each other, are in concrete construction and rise to the same height, the floor loading and cross sections of members do vary.
Even so, one would reasonably expect base isolation to yield some distinctive benefit. We can partly explain this surprising result, when we note that whilst we compare isolated and un-isolated parts at the same distance for a given train event, the isolated building has other columns which are sited nearer to the railway tracks. We know from the difference in total and direct transmissibilities, that the response of an isolated column is not wholly correlated with the input from its pile cap below. This is because vibration arises from other sources, such as, building services plant or via other paths, in this case neighbouring pile caps and columns. This implies that the isolated column adjoining the un-isolated core on gridline "C" will receive vibration from isolated columns nearer to the source on gridlines "A" and "B". This would in part explain why the isolated column on gridline "C" responds with similar magnitude to its adjoining un-isolated core, which is itself altogether further from the tracks.
It is clear that as we can fail to see any distinct benefit of base isolation against an un-isolated core, the effect of different isolator stiffness between Block 'C' and Block 'A', yields no obvious effect in this set of comparisons.
8.12.7 Comparison of Isolated Column B15 with Un-isolated Column G15
Given the site comprised of four office blocks, two isolated and two un-isolated, there was a unique opportunity to examine the characteristics of identical columns, except where one is isolated and the other is un-isolated. This section describes simultaneous measurements across Block 'C' (7.5Hz) and Block 'D' (i.e. isolated column (B15) and un-isolated column G15) and across Block 'A' (9.5Hz) and Block 'B' (i.e. isolated column (B4) and un-isolated column (G4)). Un-isolated columns on gridline G are further from the railway tracks and measured 36.6m from isolated columns on gridline B.
Figure 8.29 compares the total transmissibility across the top and base of un-isolated column G15 to similar points on isolated column B15, for a background sample. This shows that the isolated column shakes more the un-isolated column. This trend was also found to occur for columns in isolated Block A and un-isolated Block B.
Figure 8.30 shows total and direct transmissibilities between respective pile caps of column G15 and B15 to the tops of these columns for the same train event. The direct transmissibilities for this train event are overlaid in Figure 8.31, showing that whilst the isolated column spectrum is shifted to a lower frequency owing to the presence of the isolators, there is no significant benefit to be seen for the use of the rubber bearings. We can observe that the first mode of resonance for the isolated column is at 6.1Hz, which is at a lower frequency, compared to the un-isolated column, which peaks at 7.6Hz. The heights of the first mode resonance peaks are also similar. The similarity of these frequencies for an isolated and un-isolated column would be surprising. However, Figure 8.51(b) describes a theoretical analysis of both un-isolated and isolated columns, which indicates that the small difference arises because the un-isolated column exhibits a low fixed-free natural frequency.
Figure 8.32 makes comparisons between Block 'A' at a slightly higher base isolation natural frequency of 9.5Hz to its neighbouring un-isolated Block 'B', showing similar behaviour at low frequencies although some benefit can be seen from 40Hz to 100Hz.
The top of the un-isolated columns in both cases shows a fixed-free resonance mode around 8Hz. They also show that they enjoy some reduction compared to their respective pile caps. This is not often the case depicted by theoretical models, which tend to show that the top of an un-isolated column would on the whole shake more that its pile cap (see Figure 8.51; Grootenhuis, 1989).
Comparisons between isolated B15 and un-isolated G15 columns are made in the horizontal plane, longitudinal to the source, in Figure 8.33. This shows that the isolated column does enjoy some additional benefit over the un-isolated case, at low frequencies.
Whilst these comparisons of isolated and un-isolated columns are unique, unfortunately the un-isolated columns were tested under low levels of train vibration, owing to their greater distance from the tracks. This means that un-isolated columns were potentially inadequately excited, allowing background response to influence their results.
8.13 Impact Testing
A popular method of dynamic testing involves hitting the structure with a hammer. Clearly, the magnitude of impact is a function of the mass of the hammer, and its velocity when it hits the structure. Variability in the magnitude of impact is not considered a problem, as the results are normalised. There arises a system frequency characterised by the stiffness of the contacting surface, and the mass of the hammerhead, above which it is difficult to deliver energy into the structure (Ewins, 1984). The impact should ideally produce a half sine pulse, the duration of which controls this upper frequency. The stiffer the contact element, the shorter the pulse duration, which leads to a higher frequency range that is excited. However, lower frequencies were of greater interest for the testing of this structure.
A large impulse was desired, to provide an adequate signal at remote measurement points. For a given impacter mass, it is possible to increase the impulse by increasing the drop height. But this invariably causes a rebound, which should be kept well away from the first impulse, to avoid signal processing difficulties. A suitable method has been devised by Hunt (1988), where a weight with a rubber tip is dropped on an arm from a given height, where the arm is pivoted at one point. This method is however limited in its ability to excite the structure adequately at low frequencies (Cryer, 1994).
The Author wanted to investigate the possibility of using a larger mass, falling a smaller height, but on a layer of sand, as the contacting resilient element. Such a method has been used by the Author to excite bridge decks (Sharif, 1996b). This method of using a sand layer in place of a rubber pad would eliminate a rebound, and should be adequate to excite the low frequency modes.
The impact method used here meant that the mass would fall on a yielding layer of sand. The energy is imparted both into the structure, and work done in compacting the layer of sand. It was anticipated that the layer of sand would vary between impacts, and effect the delivery of high frequency energy. But it was interesting to examine if this variation between impacts would alter the low frequency response that was of interest.
It was desirable to arrange the impacts on the pile cap to assess transmissibility across the isolators. But this was not possible, as the void between the pile cap and the isolated building was too small to deploy any impact testing equipment. Therefore impacts could only be applied above the isolators, from within the basement car park.
An impacter mass of 150 kg was used and made up of ten steel plates, 300mm x 300mm x 21mm thick which were bolted together on site. The impacter mass was suspended in position via a rope off a mobile crane. A bag of sand was laid flat in the desired position of impact to give a nominal thickness after initial impacts of 50mm. Plate 8.5 shows a set up of the steel impacter mass with the sandbag in position at the base of isolated column B15. The suspension rope was severed using a hand cutter.
The drop height was varied on site until adequate signals were recorded at all measurement locations. This drop height (nominally 200mm) was then repeated throughout the tests.
8.13.1 Impact Tests - Signal processing
It was necessary to obtain the force of impact, to calculate the 'point' inertance, defined as the ratio of acceleration response at a given point with the applied force at the same point. The 'transfer' inertance is obtained when the response at a given point is divided by a force applied elsewhere, for example, the response of the top of the column to a force applied at the base.
The force of impact was to be deduced using accelerometer recordings taken from the centre of the impacter mass. The deceleration recorded, together with the impacter mass, would give force from Newton's Second Law, and Newton’s Third Law would give the force imparted to the structure. This would provide a very simple means of deducing force (also used by Cryer, 1994), but problems were anticipated.
Diagram 8.1 shows a schematic of a Brüel and Kjær DeltaShear® accelerometer. It was recognised that under static conditions the seismic mass would be in equilibrium by shear forces generated by the piezoelectric element.
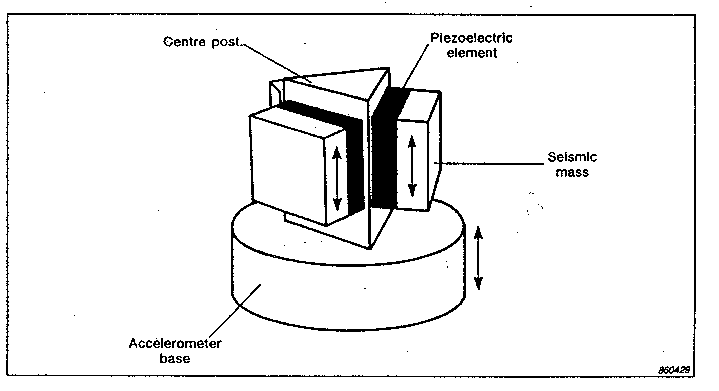 Schematic of BandK DeltaShear® accelerometer (BandK Vibration handbook) Diagram 8.1
Schematic of BandK DeltaShear® accelerometer (BandK Vibration handbook) Diagram 8.1
However, during free fall the body of the accelerometer case would fall away from the seismic mass due to its inertia, leading to a shear force on the piezoelectric material. A charge is thus produced, and reflects the force required to accelerate the seismic mass by 'g' (9.81 m/s2). This would result in a step in the acceleration output.
An ideal impulse would be a half sine wave. A dc offset and low frequency trend would cause errors in the auto spectra used to calculate inertance. Unfortunately due to cost restrictions this was the only method of force detection available to the Author. It will be apparent from the subsequent discussion that this financial restriction proved to compromise the experiment in terms of the accuracy of the force spectrum. The impulse varied in magnitude of force, and the period varied from 10msec to 20msec. This variation in period is important as it affects the upper frequency at which energy can be imparted to the structure. However, as only axial modes up to 50Hz were of primary interest, this method of impact testing was considered acceptable.
Figure 8.34(b) shows a time history of force, which shows a dc offset at the start and immediately after the impulse. The auto spectrum of force could be obtained using a hanning window of 2 seconds, centred on the impulse, and zero padded to 12 seconds, to reduce the effect of noise in the part of the time history that was of no interest. It was felt that this window would not distort the impulse or structures' response, when it was centred on the event and of 2 seconds length (used for Figures 8.45 and 8.46 which compare vibration measurements). However this method distorted the force auto spectrum (see Sharif, 1999). An exponential window was therefore used, as it had the advantage of reducing side lobes in Nyquist plots (see Chapter 5; Mercer, Turner and Kandianis, 1969; Bhaskar, 1992), and in this case would also eliminate the dc offset in force measurement at start of impulse, and weight the signal in a way that reduced the contribution of noise downstream of the impulse. The original and windowed force and vibration measurements are shown in Figure 8.34.
The shape of the impulse obtained (Figure 8.34(b)) was not in keeping with the ideal half sine pulse shown in Figure 8.35(a). There is a sloping edge and a sharper peak to the measured impulse, due to the non-linear character of loading the sand. Cryer (1994) has also observed strong ringing after such impulses, known as Gibb's phenomena.
Figure 8.35(c) shows a theoretical auto spectrum of force for the idealised impulse (Figure 8.35(a)), along with the result for exponential window applied to measured data in Figure 8.34(b). There is clearly still some distortion at low frequencies, which could be eliminated by using a boxcar window that centres on the impulse, and that matches the impulse period, as shown in Figure 8.35(b). However it would not be appropriate to apply this same short boxcar window on the vibration measurements of the impulse.
It was therefore decided for ease and consistency to apply the exponential window for impact test results involving both force and vibration signals
We can note that the accelerometer could not be placed directly on the centroid of the impacter, as it would clash with the hook used for suspending it. This would therefore cause a small error, as the deceleration would include rocking components on impact.
However, despite these points, it is interesting to examine the results, although the force results and those derived from it are to be interpreted with some caution.
8.13.2 Impact Tests - Isolated column B15 / Un-isolated column G15
Impact tests were undertaken on isolated column B15 and the identical but un-isolated column G15.
The impacter steel block was positioned directly adjacent to column B15, for impacts on the basement slab, representing the base of the isolated column. Figure 8.36 shows the impulse, along with the structure's response. Trace (f) shows the force time history, with traces (b), (c) and (d) giving the structure's response on the same vertical scale. Magnified vertical scales for the top of the isolated column and pile cap responses are shown in traces (a) and (e). We can see that the impacter mass of 150kg with a 200mm drop height produces in this example a peak force of 52kN with a pulse duration of some 10msec. This impulse produced an adequate response signal above background levels at all locations. Clearly building response measurements do not show any step seen in the force measurements, and therefore any spectral analysis of these is reliable.
There exists a delay in the response of the top of the column compared to the base at which the impulse is applied. From this delay and the distance between the two sensors (25.5m), we can simply determine the ‘compression’ wave propagation velocity as 3336 m/sec. On other columns this varied down to 2000 m/sec, representing a large range.
Impacts were again applied on the basement slab at the base of the un-isolated column G15, using the same drop height of 200mm.
The ratio of the auto spectra estimates (accelerometer response / input force) were used to derive inertance. The 'point' inertance of the base and 'transfer' inertance of the top of the isolated column and un-isolated column are shown in Figure 8.37. We can see that it is easier to excite the base of the column, when applying the force at the base. This is not surprising as the impulse at the base is attenuated three dimensionally by the structure as it travels up the building.
These results also show that an isolated column is easier to excite than its un-isolated counterpart. This has implications both to external sources of vibration, but also to internally generated forces. Therefore, the evidence that the isolated structure shakes significantly more than the un-isolated structure, due to building services plant under background conditions, shown earlier (Figures 8.29), is to be expected.
This difference in behaviour of isolated and un-isolated columns is likely to be due to a combination of factors. The impulse more easily excites the base of the isolated column which is relatively 'free', whereas it is harder to excite the base of the un-isolated column which is more effectively restrained by the stiffness of the pile. The impulse energy should also radiate into the soil more readily for the un-isolated column, whereas this path should be more inhibited by the isolators.
The Nyquist plots of the cross spectra between force and structure response were processed to allow the identification of natural frequencies and circle fits used to establish modal damping ratios, as described in Chapter 5. Figure 8.38 shows an example of the point mobility of the isolated column together with estimates of modal damping. Table 8.2 summarises a selection of modal damping ratios obtained for the isolated and un-isolated columns from an impact test.
Table 8.2 Comparison of modal damping ratios from circle fits of impact tests
|
|
|
|||
|
(Hz) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|
|
|
The damping values are on the high side at low frequencies, although not unrealistic. We can see that the damping ratios reduce for higher natural frequencies. The values in the isolated and un-isolated columns show no dramatic differences, although we cannot make direct comparisons for each value as they can pertain to different modes. The trend of a reduction in critical damping ratio with increasing frequency would imply that a hysteretic type damping model would be appropriate (see chapter 5).
8.14 Shaker Tests
Another technique to identify the natural modes of a structure is to observe the steady state response under harmonic excitation, across the frequency range of interest. This technique was used to excite the ground to understand foundation dynamics, as early as 1936 by the research organisation Degebo based in Germany. The results of similar early work are described in full by Lorenz (1960).
There are a number of ways to apply this harmonic force in such applications. The earlier systems utilised rotating eccentric masses, where force is simply proportional to the frequency squared. A disadvantage with this method is that non-linear effects can arise under different levels of strain caused by the large variation in force. Later systems utilise electrodynamic (Grootenhuis and Awojobi, 1966) or hydraulic shakers, where force can be controlled independent of frequency. Another advantage with these two methods is that they can provide any shaped forcing function. Although, for the large forces required to drive a structure, such systems are often more expensive than the simpler rotating eccentric mass exciters.
Rather than building such a unit from scratch, the Author decided to modify an existing device that is readily available to the building industry. This consists of a 'wacker' plate, used for compacting hardcore and road sub-bases. The standard unit consists of a steel bedplate on which is rigidly mounted an eccentric mass on a shaft, which is driven at a constant speed by a petrol engine, via a drive belt.
The Author replaced the engine with a dc motor, where the armature voltage is proportional to frequency and can therefore be adjusted by a dc motor controller. The dc controller was also modified to provide accurate control of frequency using a ten-turn micrometer reading potentiometer. This allowed frequency to be adjusted in 1Hz steps from 4Hz to 50Hz.
The frequency range of the shaker was limited to 4Hz at the low end, below which the forces were too small, and limited to 50Hz at the high end, above which the forces would have been too large.
Appendix 8.1 describes the shaker in more detail along with the simple test to establish the delivered force as a function of frequency. This force was derived by measuring the acceleration of the shaker, when suspended in air. From the mass of the shaker, forces giving rise to the measured accelerations were simple to deduce. The test showed the unit would deliver a quadratic force reaching 7200N at 50Hz.
The unit as conceived, produced a rotating vector force, with vertical and horizontal components. It is possible to eliminate the horizontal component by arranging for counter rotating masses, which balance the horizontal components, but amplify vertical ones. This is the principle of operation that was used in the exciters described by Lorenz (1960), and used as the basis of design in vibrators used for driving piles. However this would have required detailed modifications not considered essential.
Attaching the unit on site did present a problem, as it needed to be achieved without introducing any permanent fixings, yet given the large forces that arise both vertically and horizontally, a strong method of attachment was required.
A simple method of locating the shaker without interfering with the structure in any permanent way was devised. This entailed using three acro props, which were expanded in position, with one end pushing the baseplate of the shaker down onto the basement floor, whilst the other end derived a reaction off a concrete beam supporting the floor above.
The shaker was deployed at the base of three columns. On the isolated columns A15 and B15, to compare similar isolated columns, and the un-isolated column G15, which is identical in every other respect to B15.
Plate 8.6 shows the shaker in position at the base of isolated column B15.
8.14.1 Shaker Tests - Signal Processing
Figure 8.39 shows time histories for measurements on the pile cap, base and top of isolated column B15. The shaker is operating at 50Hz. The driving force applied at the base is attenuated significantly across the isolators to the pile cap (note different scales), but more so up to the top of the column.
There are higher frequencies evident at the base of the isolated column and pile cap, which is due to bearing noise of the shaft. There is also an indirect component coming from the flexing of the acro props, which are put into transverse motion in varying degrees, as the tests sweep across their natural frequencies.
The complete run of shaker tests was very time consuming. The charge amplifiers frequently required their gain settings to be adjusted to optimise the signal, as did the input range on the PC based monitoring system, to optimise quantisation of the signal. At each frequency, the test was sustained for at least 45 seconds, from which the end section was recorded to obtain steady state conditions. The tests continued in approximately 1Hz steps, all the way down to 4Hz.
It is important that the vibration signals from the shaker tests are significantly above background levels. Yet at low speeds, the forces from the shaker are much smaller (46N), and therefore the signals were less distinct against background levels. As a result, the test results should only be scrutinised down to 10Hz, even though the tests were undertaken down to 4Hz.
The post-processing was automated and undertaken in two ways, using programs written by the Author in MATLAB®.
One method entailed calculating inertance of the pile cap, base and top of the column from a ratio of the peak response at the driving frequency using auto spectrum estimates, divided by the respective force deduced for the shaker at each test frequency.
A simple search algorithm was devised to obtain magnitude of the peak at the relevant frequency for each test, as otherwise a peak from a neighbouring frequency could be mistaken for the forced signal. However, despite the use of this method of analysis, the inertance so derived was unable to resolve the detailed character of response at lower frequencies, owing to dominance of noise in neighbouring frequencies.
The alternative method used and presented here, entailed applying a filter which would selectively bandpass the driving frequency. The peak acceleration at various measurement points was then simply divided by the peak harmonic force at each test frequency.
The digital filtering could not be achieved using a single bandpass filter, as the high sampling rate used prevented a narrow and accurate bandpass to be designed. This could be overcome by resampling the data, at a lower rate, which would be sufficient to characterise the low frequencies. However, it was decided to achieve the bandpass filter on the original data by in effect applying two filters sequentially, a low pass and a high pass filter. This would provide the desired accuracy of 0.1dB ripple in the passband and (- 50dB) in the stopband.
An Elliptic filter was used as it provides a minimum transition width compared with the conventional Butterworth filter. Filtering causes phase distortion, and these were minimised by filtering the original sequence and its time reversed version, which averages out these phase errors, as described by Krauss et all (1994).
The harmonic response testing also allows us to estimate the degree of damping using the half power bandwidth method described in Chapter 5. This method can be used to estimate modal damping for any well separated mode.
8.14.2 Shaker Tests - Isolated Columns A15 and B15 / Un-isolated Column G15
Figure 8.40 compares the 'point' inertance of the base of isolated columns A15 and B15, which shows that it is easier to excite the outer isolated column A15, given an excitation at its base. The 'transfer' inertance is also shown to the top of isolated columns showing the same trend. Shaker tests on isolated column A15 were not extended to the full 50Hz range owing to some initial concern over the high levels of vibration that arose.
The fact that it is easier to excite the outer column A15 compared to the inner column B15, should not be surprising when we consider that column A15 supports about half the mass of column B15, by virtue of it carrying a smaller area of floor loading.
We can now uniquely compare the inertance for isolated (B15) and un-isolated (G15) columns that are otherwise identical. Figure 8.41 shows the 'point' inertance at the base of the columns, where it is seen to be clearly easier to excite an isolated column. This figure also shows a similar comparison for the 'transfer' inertance to the top, which shows that it is easier to excite the top of an isolated column at some frequencies, although at 15Hz, 26Hz and approaching 50Hz, the inertance of both isolated and un-isolated columns are almost identical. This may be due to axial modes that are common to both isolated and un-isolated columns.
We can use the half power bandwidth method to estimate modal damping ratios for the peaks obtained in the response of the top of the column, as described in Chapter 5. Where the peak response is not fully defined, we can by eye estimate straight line extensions. Some of the peaks in the response of the top of the columns and their respective damping values are summarised in Table 8.3.
Table 8.3 Peak response and damping for isolated and un-isolated columns
|
Isolated
Column B15 |
Isolated
Column A15 |
Un-isolated
Column G15 |
||||
| Frequency of selected peaks at top of column | 23 Hz | 35 Hz | 16Hz | 22 Hz | 27 Hz | 43 Hz |
| Damping for the mode | 4% | 9% | 8% | 6% | 5% | 12 % |
The sample of selected peaks shown in Table 8.3 are only an example where the modes were separated enough to make an estimate using the half power bandwidth method, although many other peaks in the response did arise.
Even so, the damping values were obtained for modes that are not all ideally independent, but are to a degree affected by nearby modes. The frequency testing in nominal 1Hz steps also did not resolve the peaks clearly. This makes use of the half power bandwidth method for estimating damping in these cases unreliable, even though the values obtained are not unrealistic.
A more reliable method of estimating modal damping, where modes are close by, is to plot the real and imaginary components of the complex response at equal frequency intervals. This method was described in Chapter 5 and used to obtain damping estimates from the impact tests. It could not be applied in this test sequence as the frequency intervals were nominally selected around 1Hz, controlled manually, and therefore not equally spaced.
8.15 'Point' Inertance of Pile Cap supporting Isolated and Un-isolated Columns
It was desirable to compare the 'point' inertance of the pile caps beneath an isolated column with that of an un-isolated column. This would provide a unique insight into how the interaction of the supported mass on a pile cap is affected by base isolation.
Comparisons of inertance using a ratio of pile cap response with the shaker applied force would not be meaningful. As in the case of the pile cap beneath the isolated column it would be the 'transfer' inertance, whereas in the case of the un-isolated column, it would be the 'point' inertance. This is because in the case of the isolated column, the force from the shaker is not the actual force applied on the pile cap below the isolator.
To obtain the pile cap force in an indirect way, the relative displacement (deduced from accelerometer measurements) between the pile cap and the base of the isolated column, was multiplied by the group isolator dynamic stiffness.
The group dynamic stiffness of the rubber bearings was simply taken from production load-deflection test curves. The tangent stiffness was calculated at the working load and multiplied by an empirical factor of 1.8, provided by the manufacturer (BTR) to deduce the dynamic stiffness. This is intended to allow for the higher stiffness that would result from the low strains expected in service (i.e. small strain cycling about a point on the overall load deflection curve leads to a steeper gradient of the stress strain loop c.f. tangent stiffness). Dynamic stiffness of natural rubber bearings loaded with carbon black are reported to be more sensitive to strain amplitude than frequency of loading (see Payne, 1962; Ahmadi and Muhr, 1999). Whilst dynamic stiffness increase slightly with frequency, it reduces with increasing strain amplitude. Sensitivity is dependent upon amount of carbon black used, being larger at higher proportions of carbon black.
Whilst dynamic tests on rubber bearings are simple to perform, the manufacturers did not have a large enough test rig to establish the actual dynamic stiffness of the bearings used. In the experiment with the shaker, strain increases as frequency is increased, and therefore would tend to reduce dynamic stiffness, which would therefore offset any increase in stiffness that might arise with increasing frequency of the loading. Given that we cannot quantify these small effects, it becomes an experimental assumption that the dynamic stiffness deduced from an empirical correction of the tangent to the load deflection curve, at the working load, is constant over the small frequency range (5Hz to 50Hz) of the test, and appropriate to the small level of strain imposed (<0.002%).
The 'point' inertance for the pile cap of the isolated column is therefore only considered an estimate, as it assumes that the dynamic stiffness of the rubber bearings is both correctly estimated, and constant in the frequency range of the test.
Figure 8.42 compares the 'point' inertance of the pile cap below isolated columns A15 and B15. The two curves are similar, although it is easier to excite the pile cap below column A15. This is not surprising as the pile cap for column A15 is formed using only one pile and carries a smaller load, whereas column B15 is heavier, and supported on a pile cap with two piles.
Figure 8.43 shows the unique comparison for 'point' inertance of the pile cap below the otherwise identical, but isolated and un-isolated columns. There is a distinct difference, increasing with frequency, whereby it is easier to excite the pile cap below the isolated column. At some low frequencies, the 'point' inertance is similar, where the presence of the isolators has little or no effect. But particularly at higher frequencies, the decoupling effect of the isolators increases. This indicates that the isolators decouple the inertia/stiffness of the supported column from the pile cap, and this decoupling is frequency dependent.
The transmissibilities for train events, reported in preceding sections, between pile cap and isolated column tells us just that, and not the insertion loss for base isolation. The insertion loss for base isolation is that benefit or disbenefit that arises between the isolated and un-isolated situation. If the pile cap beneath an isolated column were to respond more than the equivalent pile cap beneath the un-isolated column, then clearly an adjustment is required on the transmissibility results, if they are to be used to properly indicate insertion loss.
Figure 8.44(a) shows that for an applied dynamic force, the pile cap below the isolated column, would respond by in general 5dB to 10dB more than the pile cap below the un-isolated column. This result is significant, because whilst we know that the transmissibility deduced from pile cap to isolated column does not yield actual insertion loss, we can for the first time realise the size of the correction needed to more meaningfully assess the actual insertion loss from such transmissibility measurements.
This indicative adjustment has been estimated for a harmonic loading case, over a small frequency range and is shown along with the mean total transmissibility curve for isolated column B15 in Figure 8.44(b). The actual correction necessary will be more complicated, as the rail source is clearly not simply harmonic. However, an upward adjustment of 5dB to 10dB would clearly reduce the little evidence of isolation seen from such transmissibility curves, and would then show similarity to the comparative response of neighbouring isolated and un-isolated structures seen in Figure 8.28.
8.16 Comparison of Shaker and Impact Testing
We can compare the total transmissibilities from the base to the top of the isolated and un-isolated columns obtained under both shaker and impact testing.
Figure 8.45 shows a comparison for isolated column B15. Clearly we can only compare results up to the shaker test range of 50Hz, which shows a great deal of similarity with the impact testing. The size and position of the peaks are all similar, except that there is a greater divergence at 50Hz. This may in part be due to the high level of background vibration at 50Hz, which may not have been adequately exceeded by the impact test, whereas was in the case of the shaker results. Also, 50Hz was potentially a resonant mode of the isolated column (free-fixed), which under steady state conditions imposed by the shaker produces more pronounced response than did the impact test. Similar correlation between the two methods of testing arises in the un-isolated column results shown in Figure 8.46.
This confirms that the impact testing method used is acceptable for mode characterisation, is quicker to implement and therefore a very desirable technique. However, there was some variability in the results (see Sharif, 1999) and so it is important that a number of impact tests are sampled.
Even though this impact testing method has been validated, it cannot be used to assess the performance of a large base isolated building due to a train source. This is because the impacts cause vibration sources that are local and this decays three dimensionally into the structure. The rail source would in fact excite all the columns in varying degrees and with varying correlation of inputs (see section 8.10). The three dimensional decay of input from one pile under train vibration excitation would be offset by vibration coming from three dimensional decay from neighbouring columns as they shed energy through the structure. Such a return of energy from neighbouring columns would not arise as well in the impact testing case, and so would not represent a realistic simulation of a rail source.
8.17 Theoretical Analysis and Comparison with Measurements
This section describes theoretical analysis of the axial modes of a column using Finite Elements, which were modelled using the Ansys program version 5.2, running on a Pentium Pro computer. The modal characteristics obtained from simple bar models, lumped mass column models are compared with measurements.
The finite stiffness of the piled foundation was also considered, and calculated using the Dyna4 program, which is based upon the methods due to Novak et al (1974,1978a,1978b,1980,1993).
This foundation analysis program was also used to calculate the theoretical ‘point’ inertance of the piled foundations, which were treated as unloaded and loaded. These were then compared with measured values.
8.17.1 Simple Bar Models of Column
The concrete column modelled as a simple bar, with fixed support produces a fixed-free mode with a frequency of 34Hz. With resilient supports for the isolated case (target rigid body natural frequency of 7.5Hz) it produces a free-free mode at 69Hz.
It will be recalled that site column measurements showed many resonance peaks in the 100Hz range. Whilst we would not expect to model the 'real' three dimensional structure using such a simple column model, we can significantly improve this bar representation by modelling the column with a series of lumped masses at each storey height to represent the inertia of transverse beams, floors and finishes.
It is recognised that lumping all such dead loads onto the column, storey by storey, may be unrealistic. During column oscillation the entire mass of floors and beams may not be mobilised and is likely to be frequency (wavelength) dependent. Nonetheless, it is considered more realistic than just modelling the column as a bar.
8.17.2 Concrete Column - Lumped Masses - (30m length)
The concrete column was therefore modelled allowing an appropriate lumped mass per storey height (25.5 tonnes for columns on Gridline A, 51.18 tonnes for columns on Gridline B and 39 tonnes for columns on Gridline C), representing the unfactored dead loads. The concrete column was also modelled to represent its varying cross section, which becomes more slender with height. Cross sectional area is in this case relevant, as it affects the columns' axial stiffness, storey by storey under varying load conditions.
A fixed-free mode occurs at 10.9Hz for columns on Gridline A, 7.0Hz for columns on Gridline B and at 8.3Hz for columns on Gridline C, which compares with 34.0Hz for the column modelled as a bar without any lumped masses. It may be surprising that the first mode axial frequency of the fixed base column with lumped masses is so low, and in the region often targeted for rigid body natural frequencies in base isolation. For the same columns, but with an isolated base set to a rigid body vertical natural frequency of 7.5Hz, the first mode of the column is lowered to 6.0Hz for columns on gridline A, 5.3Hz for columns on Gridline B and 5.6Hz for columns on gridline C.
For the isolated case there now also exists a "free-free" mode at 19.9Hz for columns on gridline A, 15.2Hz for columns on gridline B and 17.6Hz for columns on gridline C. This compares with a free-free mode at 69Hz when the column is modelled as a simple bar. Free-free modes should be important, as the anti-node occurs at the point of excitation, and therefore are easy to excite.
An indication of the variation in axial modes that arise for different columns in the same building, due to different section sizes and storey loading is summarised in Table 8.4.
Table 8.4 Axial Modes for Columns on Gridlines "A", "B" and "C"
| Un-isolated column |
|
||
| Grid "A" |
|
|
|
| Grid "B" |
|
|
|
| Grid "C" |
|
|
|
| Isolated column |
|
||
| Grid "A" |
|
|
|
| Grid "B" |
|
|
|
| Grid "C" |
|
|
|
Differences vary and depend upon which mode is being compared. It will be shown that these differences are significant in limiting isolation obtained for a given column.
Whilst single column models, with lumped mass loading per storey height are instructive, spatially extended models are still necessary. This is because they can allow the correct inclusion of mass/stiffness per storey height from floors and transverse beams, and would model transfer of vibration from one column and another.
8.17.3 Sensitivity of 'free-free' Axial Column Modes to Isolator Support Stiffness
The natural frequency of a 'free-free' mode of a column will be affected by the magnitude of the support stiffness. We can examine this by considering three values of isolator support stiffness. The dynamic stiffness of the group of isolators under the relevant column was used in the isolated cases so far described, but two softer situations were considered, at 1/10th and 1/100th the actual stiffness values. These values do not represent any practical variation that would ever occur, but are used to assess how the isolators influence the 'free-free' modal characteristics of the column.
The 'free-free' modes vary as a function of isolator support stiffness, which are summarised in Table 8.5.
Table 8.5 Sensitivity 'free-free' column natural frequency to support stiffness (kv)
|
|
|
|
|
|
|
|
|
|
|
|
From this we can see that the 'free-free' mode established using the actual isolator stiffness is not the actual 'free-free' mode of the column were it to be suspended freely in space. This would be closer to a value of 18Hz as seen by the softer mounts case. Clearly the isolators permit a 'free-free' mode to exist, but their stiffness effects the natural frequency obtained.
It is therefore interesting to examine the 'fixed-free' case again, but this time using the finite stiffness provided by piled foundations, rather than assuming a fully fixed base. To enable this analysis, a dynamic analysis of the pile foundation was required.
8.17.4 Sub-Structure model: Pile / Soil System
The Dyna4 computer program was used to model the first axial mode of a lumped mass on a single pile, in a layered soil. A pile of 1m diameter, 18m length was modelled, with its end bearing conditions resembling the chalk stratum into which the piles were toed. Soil dynamic properties should ideally be based upon site tests, which usually involve cross-hole seismic techniques. However, in this case values were assumed based upon the Author's experience of other sites. An arbitrary vertical force was applied across a broad frequency range to identify the first axial mode. All the properties assumed for this model are shown in Figure 8.47.
The natural frequency of the pile loaded with a lump mass (appropriate to the total foundation load at pile cap level) is 19Hz, which is within the range of dominant frequency spectra caused by trains, and also close to the axial modes of the isolated column.
The finite element model of the column with appropriate lump masses per storey height was then modified by replacing the fixed base assumption of the column with the finite stiffness for the piled foundation, taken from this Dyna4 model, and implemented using a simple spring element.
Whilst stiffness and damping are frequency dependent, a single value for stiffness at 20Hz was used and taken to be 3 x 109 N/m. The piled foundation is therefore at this frequency seven times the dynamic stiffness of the group of rubber bearings used beneath this column.
A column on gridline A was modelled with a piled base, and had the first mode at 9.6Hz which is broadly similar to the first mode for the fixed base at 10.9Hz. However the second mode, with piled base is 24.9Hz compared with 29.3Hz for the fixed base.
Therefore a piled based alters the axial modes from the fully fixed base assumption. A 'free-free' mode of the column can now begin to emerge, as the pile introduces resilience and therefore a degree of freedom at the base of the column.
8.17.5 Theoretical 'Point' Inertance of Pile Cap for Isolated and Un-Isolated Columns
We can also use the Dyna4 program to calculate the 'point' inertance of the pile cap, which we can model as unloaded and loaded.
Piled foundations were modelled in such a way as to match those which were tested, namely; isolated column pile caps A15 and B15, and the un-isolated column pile cap G15. These are schematically shown in Figure 8.47, along with the concrete and soil properties that were assumed.
The pile cap below isolated column A15 is provided with a single pile, which is loaded concentrically. The pile caps beneath isolated column B15 and un-isolated column G15 are in fact identical, being rectangular and served by two piles. The column loads are applied near the centroid of the rectangular pile cap, but these are necessarily eccentric to the two piles below.
Figure 8.48 compares two versions of the theoretical ‘point’ inertance of the pile cap beneath isolated column A15, along with the measured result. One of the theoretical predictions assumes that the pile cap is unloaded (solid line), whilst the other assumes that the total mass of the column is lumped as a point load on the pile cap (dashed line). We can see that the theoretical prediction, which assumes that the pile cap is unloaded, matches the measured results.
This is an important result, as it indicates that the pile cap beneath an isolated column does not mobilise the inertia of the supported building. This arises because the isolators dynamically detach the inertia of the building from the motion of the pile cap.
We can examine if this correspondence also arises for the pile cap beneath isolated column B15, shown in Figure 8.49. When we model this rectangular pile cap served by two piles as being rigid, as we did in the case of the pile cap served by a single pile for column A15, we find there is poor correlation with the measured result. However, when we model the rectangular pile cap as flexible, we find that the correspondence is greatly improved. There are two curves which straddle the measurements, and refer to the inertance at different points of the flexible pile cap, one of which corresponds better with the measurement position used on site (see footnote to Figure 8.49).
This is a significant result, because firstly it tells us that even pile caps, which are traditionally thought of as rigid entities, must clearly be treated as elastic when multiple piles are involved, or where a pile or piles are not loaded concentrically. Secondly, the result again confirms that the measured inertance follows the theoretical inertance, when the pile cap is assumed to be unloaded. Therefore, the interaction of the mass of the supported building with the pile cap is affected by the isolators.
We can recall from Figure 8.42 that the measured inertance of the pile cap below column A15 was slightly higher than the inertance of the pile cap below column B15. This small difference was also borne out by the theoretical inertance of the two unloaded pile caps (see Sharif, 1999).
We can compare the theoretical inertance of an unloaded and loaded pile cap for columns B15 and G15 along with the measured results in Figure 8.50. We see as before, that the pile cap below the isolated column closely follows the theoretical inertance where the pile cap is assumed to be unloaded. Significantly, we see the measured inertance of the pile cap for the un-isolated column becoming increasingly divergent from this prediction as frequency increases.
The theoretical prediction of inertance for the loaded pile cap is also shown. Whilst the measured inertance for the pile cap below the un-isolated column does not follow this prediction either, it does lie between the two theoretical curves. This implies that the inertance of a pile cap below an un-isolated column is affected by the inertia of the building. But as the un-isolated column is itself elastic, its interaction with the pile cap is frequency dependent, and so cannot be simply modelled as a rigid mass on the pile cap.
8.17.6 Theoretical Transmissibilities
Column models were subjected to harmonic support motion to obtain their frequency response. Chapter 5 showed how such results are very sensitive to the nature and magnitude of damping assumed. In this case a constant damping ratio of 5% critical was assumed. That is, the solution at each frequency is repeated using a different set of constant coefficients to obtain the same 5% damping ratio through the frequency range.
Theoretical transmissibilities from a rigid pile cap to the top of an un-isolated column, and to the base and top of an isolated column are shown in Figure 8.51. With trace (a) comparing otherwise equivalent columns on gridline A and H and trace (b) comparing otherwise equivalent columns on gridline B and G (see Figure 8.1). This shows that the top of an isolated column does theoretically respond less than the equivalent but un-isolated column, except for the situation being either comparable or worse at certain frequencies. We also see that there are differences in the relative behaviour of isolated and un-isolated columns according to section size and column loading, compare trace(a) with trace(b). Note the small difference in behaviour between un-isolated and isolated columns at low frequencies (trace (b)), which was borne out by measurements (c.f. Figure 8.31).
We should note that these theoretical transmissibilities do not provide the actual insertion loss for base isolation, but aid in understanding the relative response of the structures compared to an input on the pile cap.
The measured mean (from 5 train events) of direct transmissibilities is compared to theoretical prediction for both un-isolated and isolated columns in Figures 8.52 and 8.53. Comparisons of direct as opposed to total transmissibilities are made with the theoretical model, because theory only considered the behaviour of one column. The measured direct transmissibility describes the response that is related to the input that arises on the pile cap, and should in theory exclude any contribution that arise from other paths (if un-correlated), or due to noise.
The measured mean direct transmissibility from pile cap to the top of the un-isolated column G15 shows correspondence with theory at the first mode resonance is excellent (Figure 8.52), which clearly confirms that a lumped mass column model is an adequate representation of the fixed-free mode, and the assumption of 5% critical damping ratio is appropriate. But there is otherwise very poor correspondence between the two. The theoretical prediction falls away at higher frequencies because the top of the column becomes a node to other axial and flexural modes of the column.
The measured mean direct transmissibility from pile cap to base and top of isolated column B15 are also compared with a theoretical prediction in Figure 8.53 which also assumes a constant damping ratio of 5% critical. Were we to have used a SDOF model, we would expect to see reduction begin to arise above Ö 2 times the rigid body natural frequency (see Figure 5.3 of chapter 5) equivalent to 10.6Hz for this comparison, but this is not the case here. However the MDOF model used shows correspondence up to 20Hz is fair, although the similarity is lost at higher frequencies.
The loss in similarity at higher frequencies in both cases can be partly explained as due to a lumped mass column model not being appropriate, since the interaction of floor mass is likely to be frequency (wavelength) dependent.
It is significant to note that we theoretically predict deep anti-resonances and troughs, yet these features are not borne out by the transmissibility measurements. The reason is that our theoretical model considers a lumped mass model of a single column. Whereas the actual structure is 3-dimensional, where many more intermediate modes exist, which arise from both variations column to column (e.g. Table 8.4), the presence of flexural modes of the frame (due to network of floors and beams that link the columns), and the influence of the piled foundations. Another reason for not seeing strong evidence of isolation is if the strength of train signals are low, leaving background response to dominate, which is particularly the case at high frequencies.
It is suggested that varying correlation of inputs (section 8.10), the transfer of vibration from neighbouring columns and the range of frame/foundation modes have a net effect that deep troughs and anti-resonances do not materialise. Improved correspondence can therefore only be realised from extended models of a type proposed by Cryer (1994).
8.18 Conclusions
This case study examined the relative behaviour of isolated (BTR @ 7.5Hz and 9.5Hz) and un-isolated buildings on a site, which are otherwise similar or identical.
Short circuits were found in some columns as grout leaks that bridged part of the pile cap to isolated column. Comparative measurements with neighbouring columns 'free' of short circuits did not show a dramatic difference, although there was evidence that free columns performed slightly better. It was suggested that the grout might have cracked by differential movements between the isolated structure and pile cap.
Transmissibilities from pile cap to base and top of isolated structure only began to show reduction with respect to pile cap levels above 20Hz, and therefore does not address a significant fraction of the spectrum associated with railway sources at grade. Furthermore a SDOF approach to modelling, where reduction is expected to arise above Ö 2 times rigid body natural frequency (º 10.6Hz in this case) is misleading.
Transmissibilities from pile cap to top of isolated and un-isolated columns that are otherwise identical were similar. Column models with lump masses to represent floor loading reproduced some of the measured characteristics at low frequencies, and are an improvement over SDOF or uniform bar models. Such models predict deep anti resonances and troughs not borne out by measurements. This could in part be due to weak train signal, where background response can dominate. However spatially extended models would be required to consider the range of modes that actually exist.
Comparisons relative to pile cap do not provide insertion loss for base isolation, obtained as difference in response between otherwise identical isolated and un-isolated structures. This showed in spectral terms that on the whole an isolated column responded more than an adjoining un-isolated core area. But we cannot generalise, as neighbouring structures were not absolutely identical and more significantly whilst at the same distance from the railway, the isolated column would receive vibration from neighbouring isolated columns nearer to the tracks, whereas other parts of the un-isolated structure were altogether further from the tracks.
Impact and shaker testing showed inertance of an isolated column to be greater than an equivalent but un-isolated column. This implies an isolated structure would be easier to excite, which was borne out by comparisons of building response to services noise.
Impact testing was used to estimate modal damping, which was found to be broadly similar in the isolated and un-isolated columns, and was of a hysteretic form.
Shaker testing was used to determine point inertance of pile caps which was larger for a pile cap below an isolated column compared to an un-isolated column. Measured inertance of pile caps below an isolated column correlated best with theory when the pile was assumed to be unloaded rather than loaded with a lump mass representing the dead load of the column above. In contrast, the measured inertance of the pile cap below the un-isolated column lay between the theoretical prediction under the two loading cases. Isolators can therefore decouple building inertia from interacting with the pile, and makes this pile easier to excite compared with a pile under an un-isolated building.
For low frequency vibration from railways at grade, base isolation of a large framed building using BTR was in this case inappropriate. However there have been no adverse comments, but clearly this in itself should not infer base isolation performance.

